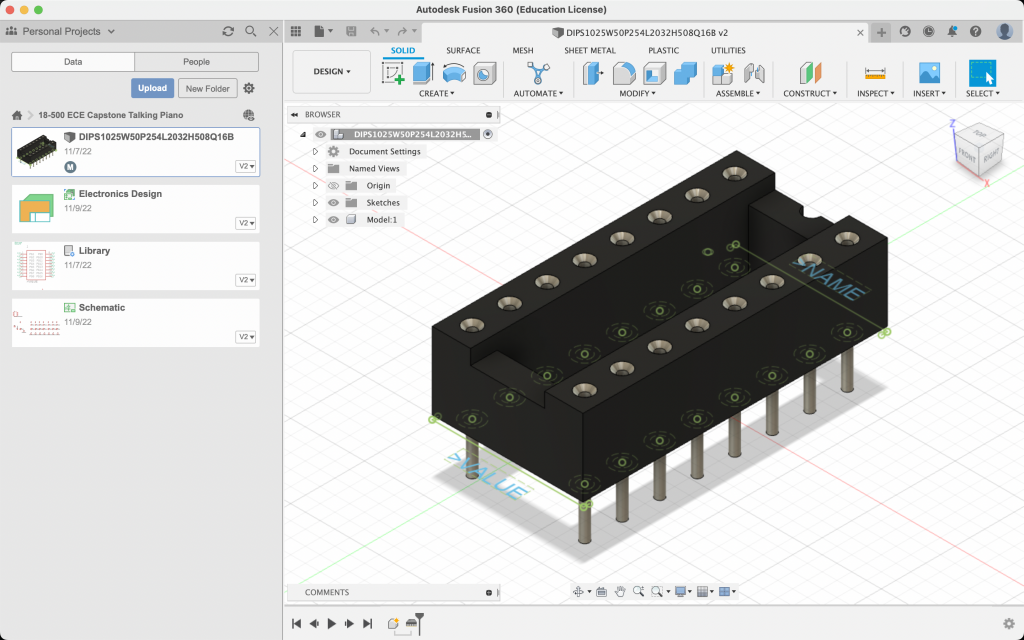
This week I started designing the PCB for the physical interface and sourcing parts from JLCPCB.com, which is where we’ll be manufacturing the PCB. Here is a list of all the parts I found. For the PCB, I had to design the receptacle that will hold the shift registers we ordered, below is a screen shot of the 3D model I generated for the receptacle.
This week we also presented our interim demo, after which we talked about some issues we’ve run into with the audio processing module. I’ll try to introduce the issue here, but some further investigation might be necessary if the reader is unfamiliar with certain signal processing concepts. I’ll try to add some links to further information where I can!
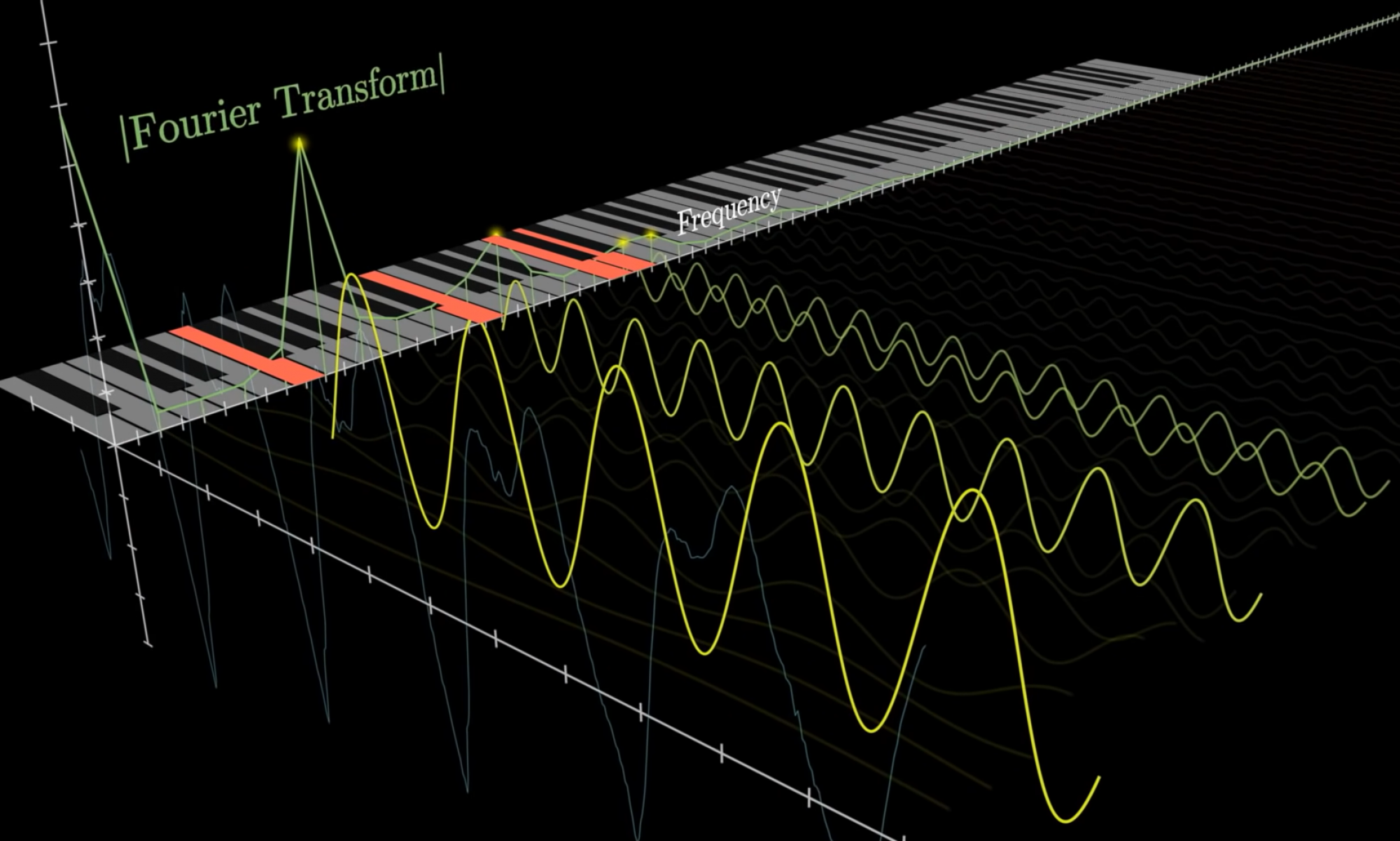
Our physical interface has a play rate, i.e the rate at which we can play keys with a solenoid, of 14 times per second. This rate dictates the number of samples we can extract from the original audio signal which is being recorded with a sampling rate of 48kHz. We’ve called these samples our window size, which results in a window size of 3428 samples per window. These are the number of samples we can use to perform the Fast Fourier Transform (FFT). One thing to note about the FFT is that our window size dictates how many frequency bins we have access to within a given window. Frequency bins are the number of evenly spaced points along the frequency domain that we can use to divide the range of possible frequencies recorded. For example, in our case with a range of 0Hz to 48kHz and a window size of 3428 samples, there are 3428 frequency bins which gives us a step size of 48kHz / 3428 ≈ 14 Hz. This means that each sample is separated by 14Hz in the resultant array we get from the FFT of our window. This is unfortunate because the step size amongst the frequencies of piano keys has a step size with 3 decimal points (e.g Key 1 that has fundamental frequency of 29.135Hz).
We’re currently investigating solutions to this issue, some of which include:
- Rounding the piano key frequencies to their nearest integer, giving our piano keys domain a step size of 1. With that we can interpolated the 3428 frequency bin range of [0, 5000] with a step size of 1.
- Filling our time domain window with 0’s
- Reducing the sample rate to around 16kHz, since it would help us work with smaller datasets, have faster computation speeds, and isolate the frequencies we care about better
I’ll be implementing these avenues and investigating if they help us with our issue at hand.