Posted on

Aditya Status Report for 2/18

This week I developed code to detect the notes within a frequency array. The code isolates a relevant portion of the array and determines the average frequency of the segment. It then applies a mathematical formula that determines the note associated with a frequency based on the reference note, which in our case is A4 = 440 Hz.

I also built the file hierarchy of a django app and began the process of integrating our starter code into it. I designed a structure to hold information for a Note object, to build a database of notes for the web app to access when it comes to sending the information to the front-end.

My plan for next week is to design and implement the process of applying the Discrete Fourier transform to get the frequency arrays which will be processed by the detectNotes() method, so that I can get a sequence of Notes each of length one-quarter beat which will be integrated with the rhythm processor to determine where each Note should begin. After these have been integrated, the Note objects will be built.

Posted on

Team Weekly Status Report for 2/18

Principles of engineering, science and mathematics

  • Short-Time Fourier Transform of a time domain signal. (18-290)
  • Utilization of frequency domain vs time domain to analyze different signals for different purposes (18-290)
    • Time domain for rhythm processor: we can analyze the start of a new note by detecting a sudden drop and rise in energy. This will allow us to detect the different length of each note and when a note ends leading to the start of a new note. 
    • Frequency domain for frequency processor. Thanks to the Short-Time Fourier Transform we will be able to detect the average frequency over a specific interval (of the length of our box size in the STFT), and with this frequency we can detect what note it is being played.
  • Signal-to-noise ratio (18-100, 18-290)
    • Our system will reject audios that have a poor low SNR.
  • Object Oriented Programming (15-112)
    • We will need to have different objects in our code for the characteristics of the fourier transforms, notes, audio files, etc. 
  • Web Applications (17-437)
    • Our system will require a web application for the users to access the system from their laptops. 

Significant Risks 

Unfortunately this week we have fallen a little bit off-schedule. One of our team members was sick for the whole week, therefore they were unable to make progress on the project. We also had issues with searching for software libraries that will allow us to test our frequency processor due to having installation issues which took longer than expected. For example, we tried installing a library called CREPE in python that would give us the frequencies given an audio sample. We were planning on using this to compare it with our frequency processor output. The problem is to install this it required tensorflow and installing tensorflow was giving us a lot of issues. After unsuccessfully trying to install CREPE, we decided to move away from CREPE and found another library called Parselmouth which was very easy to install. Therefore, we will be using Parselmouth to test our frequency processor. This library allows us to get all the frequencies of a specific audio, therefore we could compare the output of this library to the output of our own processor. 

Therefore the risk that I see is us not being able to finish everything on-time. However, I think that by putting in more work in the upcoming weeks we should be able to get back on track. Working on the Design Review helped us reorganize ourselves and adjust our plans based on the setbacks of this week.

Changes made to design 

We have not made any changes to our overall design, but we have worked more on developing the specifics of the sub-processors and the transcription engine. We have determined a method of isolating the pitches at specific segments of the signal, a binary mapping system to determine when a new key-press occurs, and a design structure that contains this information in a way that is easily comprehensible by the VexFlow library.

Updated schedule

We have updated our schedule a little bit, to make the process of building the sub-processors more concurrent and adding some sections for the user-testing part of our project.

 Photos about progress 

Parselmouth manually examining/testing of pitch over time compared to SciPy (previous method). Parselmouth is more accurate and comprehensible.

 

Posted on

Kumar Status Report 2/18

This week was a mixed week for me. From last weekend until Wednesday afternoon, I was struggling with intense gastritis and stomach issues. Hence, I missed almost all my classes and wasn’t really able to work on a screen. Since then, I have been playing catch-up in regards to the front-end work. I created and installed the django-app we will be using, and set-up the repository, as can be seen in this picture. I am now working on building the HTML pages that we will use that will have file upload and a welcome screen, etc.

As the pitch processing is the crux of the main challenge we expect to face, I also assisted Aditya and Alejandro with the Python library CREPE, which required TensorFlow. After much struggle we all had to abandon this task, and the other status reports explain how they moved forward.

 

Finally, I worked with my teammates on the design review slides in terms of ideating on testing methodologies, technology we will use, software implementation plan, etc.

 

I would say I’m slightly behind task given the time I lost due to my sickness (had to request extensions in all classes and received a UHS note). I plan on getting on track by redirecting all my focus on the django front-end and working to re-acquaintance myself with the models.py and databases in django.

 

Posted on

Alejandro’s Weekly Status Report for 2/18

The following courses were helpful in the design principles used in our project:

  • 18-290: Fourier Transforms, Frequency Domain vs Time Domain Signals, Signal to Noise Ratio.
  • 15-112: Object Oriented Programming.
  • 17-437: Web Applications.

During this week I mainly focused on trying to find software that will help us developing the frequency processor. Last week I found out that the pitch function from MATLAB would be quite useful to have to test against our own frequency processor. The purpose of this function is when given an audio signal it would return to the user all the frequencies found for that signal in the right order. Therefore, we can compare this to our own frequency processor to determine how accurate our frequency processor is. 

The problem is that we will need to write this code in python since we need to build our web-app utilizing Django. At first, I tried utilizing a public library called CREPE. However, it was really hard to install this library, and I was not successful in doing so. I tried for 2 days to install it, but the library required me to install TensorFlow and it was causing me too much trouble, as well my teammates. 

I decided to look for other libraries and I found another one called Parselmouth. This library was easy to install and also has a Pitch function to determine the different pitches given an audio file. The software seemed to correctly detect the frequencies given a couple of files that we had. Therefore, we will be utilizing this for testing our frequency processor. 

These are the outputs of a C-note and a C-scale: 

I also have been working with my teammates in laying out all the content for the Design Review, as well as setting up the database for our django application.

I would say my progress is on-schedule. There have been some modifications to our Gantt chart and I will be focusing this upcoming week on researching how to do the rhythm processor, as well as preparing to give the presentation for the Design Review.

Posted on

Kumar 2/11 Progress Report

This week I focused heavily on the design presentation slides – for example working on the Gantt Chart and figuring the best division of labor.

 

I then began researching and refreshing my skills regarding the front-end webapp which will be designing, as Alejandro and Aditya started working on the back-end. This is reflective of all the overall tasks and division of labor we had outlined in our proposal presentation. I did this by refreshing my skills with a basic Django App tutorial that I found online from  https://docs.djangoproject.com/en/4.1/intro/tutorial01/ and various Youtube sources.

 

Finally, after some exploration, I’ve attached two screenshots of the layouts and user interfaces that we roughly hope to replicate with our final app design based on the apps “Voice Recordings” and “Genius Scan”. 

Posted on

Alejandro’s Status Report for 2/11

This week I helped on creating the proposal slides for the presentation that Aditya gave on Wednesday.

I was also supposed to think about the design of the data structure for the audio file in our code. I thought that we could have the following data structure for the audio file. The data structure would contain a field containing the length of the audio in minutes, the sampling rate of the audio in samples per second, the number of samples taken throughout the whole audio, and a field containing an object which would be containing the content of the Short Time Fourier Transform for our audio.

class audio {

length

samplingRate

samples

STTF{}

}

I also researched into some helpful tools that we could utilize for our frequency processor. I found out that MATLAB offers a function called “pitch()” that when given an audio file input it will give us an output containing the frequencies of the audio. This would be ideal for us to use it to detect what note frequencies are being played at a certain time. This is the output of the function for a C-scale audio for example 

and this is the output for a constant c-note

The only issue is that when the audio goes quiet we get inconsistent frequencies like for the first image at the beginning and at the end. Therefore, at moments of silence we would have to ignore the output of this algorithm and this might be a challenge we have to deal with in the future.

My progress is on schedule, and next week I will be focusing on designing the data structure for the Short Time Fourier Transform as well as helping my team in integrating the frequency processor in the back-end in Python.

 

Posted on

Team Weekly Status Report for 2/11

The most significant risk for our project right now is the timeline. We have a very strict timeline where we aim to complete much of the research and outlining process for the signal processing within the next week (two weeks total including this week). While we feel it’s a realistic goal, we have found that the process can be very time-consuming and our completion of our research for this week was nearly overdue. The difficulties can compound when it comes to implementing the research in the back-end of our web app, because we have to format the outputs in a way that the computer can process, not simply charts and visual representations that we have been working with for now. There are also elements of our signal processing design that may require further work when we reach the coding stage, as Python has limited signal processing libraries compared to MATLAB, where most of our research is done. Aditya found that after determining the parameters of the STFT of the test signal in MATLAB, he had to work out a different set of parameters while working with the SciPy library’s stft() method.

 

As we have only just completed the design process process and currently we are on track with our schedule of implementation, we have not required any changes to the existing system design.

 

These are some pictures of the frequency algorithm detector Alejandro found in Matlab to detect frequencies. The first image shows an audio of a piano playing the c-scale and the second one is a constant c note. We can see the x-axis being the time doing and the y axis the frequency domain.

 

Our project includes considerations for education and economics. We realize that a lot of people might want to have access to a free easy to use music transcriber. Most transcribers out there come in the form of applications and require subscriptions to them to be able to use them. With our webapp anyone could use it for free. It would especially be useful for teachers who might want to show students the transcription of a specific song they are playing in class for example. It would also make it efficient for people to have a tool that can transcribe short monophonic audios for them, instead of just having to manually transcribe it themselves. Finally, it increases accessibility to music, especially those who may not have the time, financial resources, and other barriers. This may be especially helpful to students and teachers in low-income communities as often their arts and music programs are the first to get cut.

 

 

 

Posted on

Aditya’s Status Report for 2/11

This week I worked on determining how to use the Short-time Fourier transform to depict an audio signal in both the time and frequency domains at the same time. I recorded several basic audio samples using my iPhone of me playing the piano; one was a C note held for a couple seconds, another was a C scale ascending for five notes. I started by using MATLAB, as that is the system most designed for this kind of signal processing and plotting. I wanted to determine how to isolate only the relevant frequencies in a signal and determine at what point in time they are at a relevant magnitude.

I used this method from the scipy library to generate the STFT:

f, t, Zxx = stft(time_domain_sig, fs=sample_rate, window = 'hann', nperseg = sixteenth, noverlap = sixteenth // 8);

The key difficulty here was determining the parameters of the STFT. The functions asks us to pick a window shape, as well as the size of the window and how much the sliding window should overlap. I attempted to use a rectangular window at the size corresponding to one second of the audio clip, but I realized that a smaller-sized Hann window worked better to account for the signal’s constantly changing magnitude. I also assigned a window size of 1/2 the sample rate, because each note of the scale I played for about 1 second, meaning I would have 2 windows applying the Fourier transform to each note. I translated this code to a python script and wrote a method that takes a file name as input and generates the STFT.

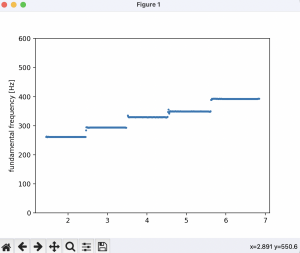
This code resulted in the following graph:

You can see the earlier pulses are more accurate to the start of the pulse than the later ones, suggesting a smaller window is needed to get accurate DFTs. The cost of this accuracy is a slower and more redundant process of obtaining the frequency-domain representation of the signal.

I am on schedule for researching the frequency domain representations of the audio signals, because my goal was to have a proper back-end representation of the signal’s magnitude at relevant frequencies. My plan for the next week is to fine-tune this data to be more accurate and write code to detect which frequencies correspond to which musical note and generate a dictionary-like representation of the note, it’s magnitude, and it’s length. My deliverable will be the python code which outputs an easily comprehensible list of notes in text form.