This week I majorly worked in integrating my path planning algorithm with Zeyi’s user interface. In the process, we identified some bugs with the algorithm and I fixed them.

First bug was with the replan() function. I ended up referencing some local variable that only existed in my version of the path planning algorithm (duplicate variable names in testing code). This created a problem on Zeyi’s side where replan() only works for certain pairs of nodes. It was a rather easy fix to change the name of the variables used in within the scope of function replan().

The second bug was a bit more tricky to fix. After discussion with professor last week, we came up with the diagram below to represent a more realistic shopping mall. As shown in the picture, there are five shelves and lines drawn in between and around the shelves are the line that our cart would follow. Node 1 to 7 are shopping nodes at which the cart will stop and have the user grab their items, node 0 is where user pickup the shopping cart and node 7 is where the checkout is. The other 10 nodes are there for convenience of the planing algorithms. Every edge on the map has the length of 2. I chose to equally space out the shopping nodes (node 1 – 7) between pair of two shelves to maximize coverage and minimize number of nodes needed.

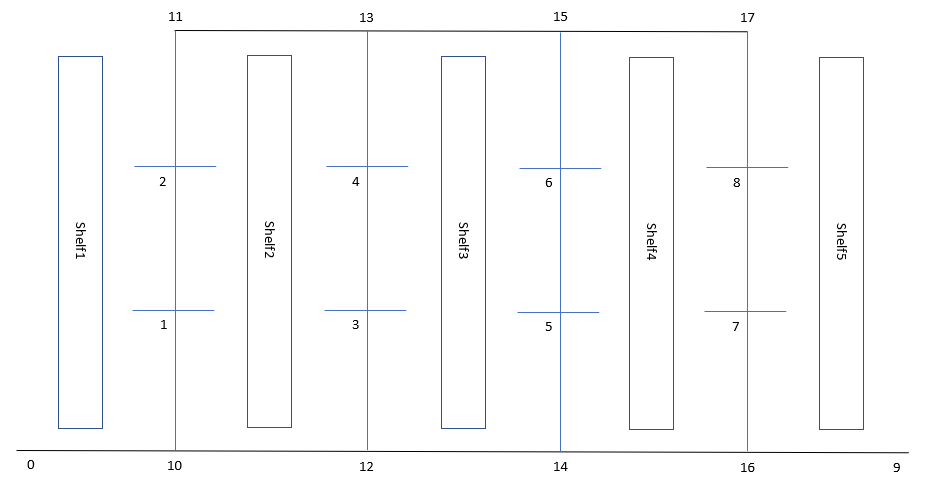
We quickly realized a problem where the algorithm seems to never visit node 11, 13, 15, and 17. For example, if we were to have the cart visit 2, 4, and 6, the most optimal route would be 0->10->1->2->11->13->4->13->15->6->5->14->16->9, with a length of 26. However, the algorithm returns 0->10->1->2->1->10->12->3->4->3->12->14->5->6->5->14->16->9 with a length of 34. I realized this was an edge scenario I did not account for when I added the capability of starting and ending on different nodes. Before choosing which shopping nodes to visit, the algorithm starts with the shortest path between origin and destination. In the case above, that would be 0->10->12->14->16->9. The algorithm then starts to repeatedly selected from the required nodes that can be inserted into the current route with the least cost. The problem occurs because the algorithm only considers the possibility of inserting in a pair of adjacent nodes. In the above case, when the algorithm selects where to insert for the first time, it only considers between 0 and 10, between 10 and 12, between 12 and 14, between 14 and 16, and between 16 and 9. By doing this, the algorithm loses the ability to correct previous route. In other words, if any edges of the shortest path from cart pickup to checkout happens to be not on the optimal route overall, the algorithm fails to find the optimal route. This was not a problem when origin and destination were the same point because the implicit origin -> origin edges is always guaranteed to be in the optimal route. And the simplification of only considering pairs of neighboring nodes as candidates for insertion served as a justified way to increasing performance. But when it comes to starting and ending on different nodes, the above bug happened precisely because edge 10->12 and edge 12->14 are in the shorting path from node 0 to node 9 but are not in the optimal route. I immediately thought of a fix to this bug. I can revert back to considering all possible pairs of node as candidates for inserting another node. But before diving right into implementing this fix, I, out of curiosity, wanted to see whether the problem persists if I do start and end on the same node.

As it turned out, another problem emerged. What should I do when I reach a equality? What if two to-be-added routes have the exact same cost? To address this problem, I added the capability of keeping track of how many new (not in current route) nodes a to-be-added route visits. If two or more viable to-be-added routes have the same length, the one that visits the most new nodes is the best simply because choosing this one opens up more possibility in the future. In other words, doing this decreases, to the most extend, the possibility that an optimal route turn out to be not viable based on the current route. I do not have a concrete example to showcase this problem.

As to actual implementation, I loop through all pairs of nodes in the current route. If the pair does not have any required node that is visited only once in the current route in between them, it is considered a viable pair. If such a pair is selected, the original sub-routine in between the pair is deleted and the path to reach and come back from the new node is inserted in the place of the removed sub-routine.