Posted on

Xiao’s Weekly Status Update 04/01/2023

The first half of the week I was focusing on getting a test bench style hardware setup.

The above test bench was what I ended up with. It can be connected to any wifi network for our team members to use anywhere for development. At this point, hardware setup for the preliminary demo is all complete. IMU is able to output raw data (acceleration, gyroscopic, magnetic, each with 3 dof). ADC reads raw voltage input from the potentiometer. All 16 buttons work.

On Monday I transferred this setup to my team mate Qiaoan for coding and testing of gyro algorithm. Over the course of this weekend I will coordinate with him to get the hardware control part all working as a whole.

As the preliminary demo is imminent, I think my part is right on schedule, but could have gone a little bit faster.

Posted on

Team Status Report for 03/25/2023

Last week all the team members are continue designing and implementing both hardware and software. Our team members also gathered together to discuss what we have learned from the ethics assignment and considered worst-case scenarios when our product is used badly.

The hardware system part has made progress in wiring and is expected to be finalized by this weekend. The gyroscope system has generated the design on processing raw data from angular velocity and accelerations to degree output. For now the workflow of geroscope system is finished with design part, the next step will be start testing once the hardware system is ready. The program on RPi works well for now but there are still some issues with the packages on the PC that needs to be resolved. We are all working on our pieces so a reasonable prototype can be put on during the interim demo.

Our team is still a bit behind schedule as the interim demo is approaching. We need to have more meetings next week to synchronize our progress and discuss in what way we should present our progress during the interim demo.

Posted on

Yuxuan’s Status Report for 03/25/2023

This week I’ve successfully installed and tested the Bluetooth module on Raspberry Pi. It’s able to act as a Bluetooth client or a server. However, I’m still struggling to get the Bluetooth module to work on windows PC. The program will have OS errors only when calling certain functions. I’ve spent a significant amount of time following the solutions online, including installing Windows 10 SDK and installing build tools from Visual Studio to compile C++ code, but the error still exists for now. Some progress is made when testing with the controller emulator as the Xbox tester program can accurately detect the emulator’s input from the tester program as shown below.

https://drive.google.com/file/d/1a4xpNfXjKo9RPMEPMMTBzyBwYentaU0O/view?usp=share_link (Couldn’t upload images for some reason)

Next week, the primary focus will still be making sure the Bluetooth connection can be established. I’ve just found another solution that simply uses the socket library with Python 3.9+ on Windows 10 to establish a Bluetooth connection. There are only a few discussions about it online but still worth a try. The next step will be talking with Xiao and Qiaoan so we can agree on the data format to be sent between RPi and PC. My initial plan is to use json. I’m still a little behind the schedule due to the problems with bluetooth package on PC. I will catch up as much as possible to make sure the Pi can control the game on PC before interim demo.

 

 

 

 

Posted on

Qiaoan’s Status Report for 03/25/2023

This week:

For unknown reason wordpress is stopping me from uploading images. It says The uploaded file could not be moved to wp-content/uploads/sites/230/2023/03. I’ m sorry about this and will try to add pictures back once this gets fixed.

The gyroscope system is still waiting for hardware to be ready for testing. This week let’s discuss how we can use the gyroscope readings to generate the degree output we want to feed in our functions from last week’s report.

The gyro section of data from the gyroscope should be the point we want to focus on. The reading is based on angular velocity in degrees per second. The key point is to transform this velocity data into the angular position.

The pseudo code solution could be like this: (I want to upload image for this but wordpress does not allow me to do it)

# We keep running the degree calculation in a loop
while True:
  curTime = time.time()
  deltaTime = curTime – prevTime # Get the time difference from the last reading
  deltaDegree = dX * deltaTime
  degree += deltaDegree
  if degree > 360:
    degree -= 360
  if degree < 0:
    degree += 360
This seems to be a working example to calculate the angular position. However, such method will be affected by errors and will get more and more inaccurate as time passes. Without testing I cannot determine how severe the problem could be, but we can use accelerators to calculate the current angles to calibrate the degree output.
I have a picture to explain this, I will add it with explanation after the bug gets fixed.
Assume we read accX, accY, accZ from our raw data. If we plot the direction R shown by acclerometer on the x, y, z space, and we want to map the vector on to xy, xz, yz plane as accX, accY, accZ (maybe normalize them). In our case, suppose the degree on yz plane is what we want (aka we want the reading of x’s degree), then we can easily know that cos(x) = accX/R, which means we can get x’s angle by arccos(accX/R). Then we can know the exact degree reading at the time we want.
Both two cases stated above can be used. The way based on gyro data seems to be easier, but the accelration based method is much more accurate. I will test both methods then the hardware is available.
Posted on

Xiao’s Weekly Status Update 03/25/2023

This week I have been working on completing the hardware wiring of our project. I set out planning to connect every breakout board on a piece of breadboard, and attach everything to a temporary 3D printed back plate for easy transportation.

I encountered some problems with I2C buses on the RPi at first. As our power management, gyro, and ADC all use I2C (4 addresses in total), It presents a heavy load on one single bus. What happened was that one of the addresses for power management would keep disappearing, leaving the power management board inoperable. I later solved it by creating a second I2C bus using two extra pins on the RPi, and connecting the power management board to that new bus separate from the gyro and ADC. ADC is now wired up with the potentiometer.

On Sunday hardware operation code will be finalized, and pushed to GitHub. Then I will give the completed hardware system to my team mates for  the software side of things.

Posted on

Team Status Report for 03/18/2023

Last week all the team members are focusing on our primary goals to build or design the components of our tasks. We also spent time individually completing the ethics assignment.

The hardware system has built some successful demos of wiring and buttons. More progress on gyroscope and potentiometers will come soon by this weekend. The gyroscope system has detailed the function designs for the tunning and mapping of gyroscope readings. As the Windows laptop is received this weekend, there will be more developments on software by this weekend, though now it’s a little behind the schedule. Based on the discussion last Monday, I hope the current design of functions should provide a clearer view and explain the reason behind better. We can start running tests on this once the hardware is ready.

The team is a little bit behind the schedule considering the interim demo will be on the beginning of April. We are not sure about if the tunning design is a possible approach to solve the problems we have and only testing on hardware can answer this question. We should start testing as soon as possible.

Posted on

Yuxuan’s Status Report for 03/18/2023

This week I spent some time reading the ethics papers and finishing the ethics assignments. I received the Windows PC this weekend and was trying to run the demo programs using the packages specified in the design. I also ordered a second RPi for pure sensor and software testing purposes. The PC also matched the minimum requirement to power up the game. I’m a bit behind the schedule this week as projects in other classes due this week took an unexpected amount of time. For next week, I will spend more time catching up on running and developing the programs based on the demo program on PC so that it can establish the Bluetooth connection and read data from the game.

Posted on

Qiaoan’s Status Report for 03/18/2023

This week:

For the function to migitate the handshaking of users, based on the Gaussian filter model I mentioned last time that help generate a diffused image by getting weighted average value around a certain point, I would like to generate the ouput by a weighted average of a series of x, y, z readings from gyroscope.

Suppose we use x_n, y_n, z_n for note the x, y, z reading from the gyroscope at a certain time, and a_n, b_n, c_n for their weight. Then the output degree should be a result of combination of x, y, z reading from several previous readings that doesn’t differ very much as follows:

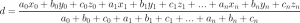
The target of tunning should be determining the value of n that indicates the number of previous readings that we want to use, and the a, b, c values to determine the weight of readings from x, y, z and based on the time of the reading (which means newer readings will have higher weight).

 

We will then talk about the logistic growth function that maps the gyroscope reading to output to the game, I have tried several possible combination of parameters. The function can be written as:

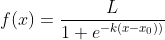
L means the range of our data, here since our degree output should be 0-180 degrees in each direction, so for the f(x) of each direction we define L=180.

k means the logistic growth rate, or we say the steepness of the curve, finding the correct value of k should be our target when tunning the steering wheel.

x_0 means the x value of the sigmoid midpoint. Here $x_0$ = 90 since we want the range to be 0 to 180.

I have tried several k values for this function to generate the mock output graph. Determining which k value to choose will depend on our testing result after the hardware is built. The graph is shown below:

The workflow of the gyroscope system should be defined as first reading the raw data from gyroscope and store them in a first in first out list of n readings. Then use the n readings to generate the weighted output and send the result to the logistic function to map the reading to the final output.

 

Posted on

Xiao’s Weekly Status Update 03/18/2023

This week I have been focusing on hardware building. Following last week’s experiments with the battery module, now I have got it working with complete python API for charging status, charge level, and so on. Charging is via USB-C and so far works as I expected.

Additionally, I 3D printed a test case for a 4×4 button matrix and wired it up. Code has been written with python, which stores the buttons’ status in an array that’s updated with every button press.

At the time of writing this status update, I am working on wiring up the gyro and potentiometer and ADC. Expected to be finished this weekend.

If all these features are implemented during this weekend, then we’re still on schedule. If for any reason hardware implementation takes too long, I think we’ll reconsider whether it is necessary and viable to design a custom PCB, or do we just use hand made wiring.

Posted on

Team Status Report for 03/11/2023

The past 2 weeks, including the Spring Break, had mainly two focuses. First one is to reorganize work assignments to our team members and get the design report written and submitted, and the second one is to order the parts and start building hardware and testing software.

The design report was a big challenge for us. We stupidly ignored everyone’s advice on starting early, and left ourselves with barely enough time to finish the report. We did try our best to gather every piece of information we could on the parts chosen, and documented every step in coming up with our design. The truth is, we messed up because we were all too busy with the sudden workload increase from multiple midterms, and we were focusing perhaps a little bit too much on actually building the device, rather than writing the report.

Schedule updates:

Hardware is on schedule. We expected delays during the spring break, but it turns out the parts did arrive very quickly. Building and testing has begun ahead of schedule.

The software is mostly on schedule. We are beginning to try installing and running demo programs using the Python packages we have identified in our design review. During the process, we went through challenges in installing as some packages are not maintained and stable. Alternative solutions have been experimented and we aim to run demo programs successfully next week.

The gyroscope system is mostly on schedule. We have came up with initial designs to implement the system. We have started writing the python code based on our design for the tuning functions. Though we cannot start testing the design without the hardware, we can draw graphs with mock data to see the output of the function.