Posted on

Shiva’s Status Update for 04/12

This week was all about collecting experimental data for Udit’s simulator.

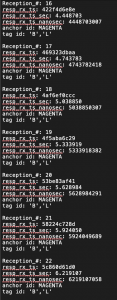
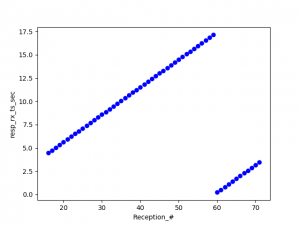
At the beginning of the week, I connected the Decawave TAG to the Raspberry Pi and logged timestamp data from the chip on the Raspberry Pi. I also wrote a Python script to parse logged data from the tag and graph the periodicity between its transmission pulses:

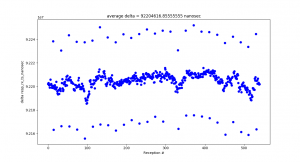
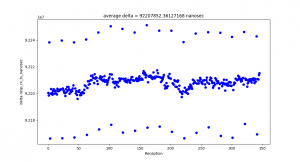
This graph depicts the time between each consecutive reception of a tag pulse by the anchor. The tag and anchor are 1 meter apart, and the tag is programmed to pulse once every 100 million nanoseconds. Note the pattern of outliers above and below the main timestamp pattern.
This graph depicts the time between each consecutive reception of a tag pulse by the anchor. The tag and anchor are touching (i.e. 0 meters apart), and the tag is programmed to pulse once every 100 million nanoseconds. Note how the pattern of timestamps, with its outlier patterns, is nearly identical to that of the previous timestamp graph.

I observed a consistent pattern of timestamp outliers. Additionally, even though the tag was programmed to only pulse once every 100 million nanoseconds, the average time between pulse receptions was 92 million nanoseconds. At first I thought the issue might be on the anchor’s end. However, when I logged the transmission times directly from the tag, I observed nearly identical results:

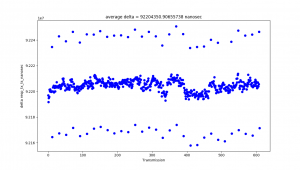
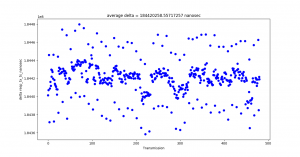
This graph depicts the time between each consecutive pulse from the tag, which is programmed to pulse once every 100 million nanoseconds. Note the pattern of outliers above and below the main timestamp pattern.
Here the tag is programmed to pulse once every 200 million nanoseconds, but the pattern of outliers is still vaguely present.

I am not yet sure what the source of these problems are.

One source may be the Decawave’s API, which zeros out the low 8 bits of its internal clock automatically to store the timestamp in a 32-bit format. This means that the time counter is only accurate to within 8 nanoseconds of the true transmission time. This problem may be compounded by the Decawave clock’s low rollover time — the system clock is only 2^40 bits long, and each bit of Decawave time is about 15.65 picoseconds of real time. This means that the clock zeros itself out every 17.2 seconds

To investigate further, I wrote a script to read the tag’s data in real-time and insert the Raspberry Pi’s own system clock time into the log to compare. However, this script does not work yet; a bug that I think is caused by non-atomic read/write operations means that the script prints the Pi’s system clock into the middle of the Decawave log, scrambling the log results and making it impossible to parse consistently.

In the second half of the week, I tried modifying an example TDOA tag code provided by Decawave to communicate with the anchor code I had written, but had no success.

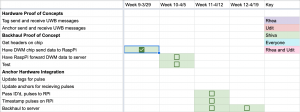
This is a bit of a switch-up on the Gantt chart. Originally, I was going to have the Raspberry Pi forward timestamp data to the multilateration server and test out the program:

However, we shifted gears to accommodate our midsemester demo. Udit implemented an ideal multilateration algorithm to show for the demo, which did not need that info. So I worked on passing the tag and anchor IDs to the Pi and timestamping the pulses directly on the Pi.

Next week, I will continue investigating these problems, fixing the bugs in the RPi timestamp program, and working with Udit to pass realistic timestamp data to his multilateration program. Since I got some of next week’s work done this week, I am still on schedule.

Posted on

Team Status Report 4/5/20

We finalized handing all the hardware we had over the Shiva and ordering more of our final hardware from Quinn to Shiva. He was able to use UART to export data from decawave radio into RPi (no longer need SPI since hardware requirement are lessened). He can now read data into the RPi and timestamp.

Shiva has MANY tests to run and data to collect. First he will use a stationary tag and stationary anchor to measure various errors and reliability. We want to see the difference between theoretical pulse transmission time differences and the differences in reception. We want to measure both the precision of the reception differences as well as the absolute difference between it and the transmission as an offset in our server code. We want to also do these tests by first timestamping in the Decawave chip and then in the raspberry Pi to see if we see which measure is more reliable. He can move on to looking at reliability with 1 stationary tag and 2 anchors and test differences in Non-LOS settings.

These experiments will be used to validate the the simulated error we will add to the hardware simulator program. If our simulator has the same percent errors as Shiva reports, we can safely validate our simulator as a way to scale our project and test the success of our Kalman smoothing and Gauss-Newton approximator.

Rhea and I have been precisely been researching and implementing those just mentioned algorithms.

We hope that we can have a basic demo with Shiva’s error graphs + Udit ideal simulation + Gauss-Newton localization by Wednesday.

Posted on

Udit’s Status Report 4/5

This week’s focus was trying to fully understand the mathematical approach for my localization software.

I genuinely spent >10 hours reading papers. Based a lot of research and looking at results, I feel confident that our best approach right now is the following.

  1. Simulate player movements on a bball court in a variety of patterns and speeds (Straight line, zigzag, random, circular).
  2. Use the simulated distance between anchors and player to calculate TOAs at each anchor
  3. Send data to server program via sockets
  4. Calculate time differences (Taus) and other measurements
  5. Use the iterative Gauss-Newton method to solve the set of non-linear hyperbolic equations by least squares approximation to get (x,y) location with least residual
  6. Smooth these values by using a recursive extended Kalman filter

We are working to start off implementing this with perfect data from steps 1-2. Shiva is working on collecting experimental data from the hardware to give us an idea of high error and consistency will be in reading these numbers. We will add in simulated error based on that experimental error as our next step.

Once we get this stack working with decent success on simulations, we can replace steps 1 and 2 with the real hardware with Shiva sending packets from his simulated setup to our server code.

Step 5 is what I am in charge of and step 6 is what Rhea is in charge of.

I spent many hours reading multiple papers that offer strategies to solve the equations needed in step 5 but typos and slightly incorrect equations has slowed down the process. But here is the math I have thus far:

For each anchor i there is a (x_i, y_i) known location with an unknown (x,y) tag location.
R_i = v*T_i where v is speed of light in air and T_i is the TOF from tag to anchor i (unknown value)
tau_ij = T_i-T_j (tau is known because you can subtract timestamps)
R_i-R_j = v*T_i-v*T_j=v(T_i-T_j)=v(tau_ij)
Via algebraic manipulation, plugging in the distance formula (R_i = sqrt((x_i-x)^2+(y_i-y)^2)), and using 2 anchors as a reference, you get an equation

alpha_i*x+beta_i*y+C_i = 0 for i in {3,4} where alpha, beta and C are values calculated from v, tau_1i, x_1, y_1, x_i, y_i, tau_12, x_2, y_2 (which are all known constants or values from data).

alpha_i*x+beta_i*y+C_i = 0 for i in {3,4} gives us 2 linear equations with 2 unknowns that can be easily solved using an inverse matrix assuming perfect data. Because we don’t have perfect data, we have to use the hyperbolic equations and use a Gauss-newton least squares approximator.

I don’t fully understand the least squares method (especially how to implement it in code) and what are the exact hyperbolic equations that need to be approximated. Right now, I don’t see why we can’t estimate using the linear equation but that is my task for the next day or so.

Posted on

Shiva’s Status Update for 04/05

This week, per our revised Gantt chart, I was able to send data from the Decawave chip to the Raspberry Pi over UART. Although I also wanted to transmit data over SPI, the SPI functionality in the Decawave chips were poorly documented. Their guide referenced a test program that was not actually included in the Decawave firmware and software bundle download. Thus, after conferring with my team, we decided to stick with UART over USB rather than waste time fiddling with SPI.

This week, now that I’m able to get correct timestamp data, I will be setting up a system of multiple Raspberry Pis attached to Decawave chips and collecting experimental data on metrics that can be fed into the simulator Udit and Rhea are developing.

Our team’s progress is still on schedule.

Posted on

Rhea’s Status Update 4/5/2020

At the end of last week Udit suggested another paper for us to use as reference for our multilateration software.  So I started working on understanding the paper, but while going through the math I noticed that the hardware set up was different than what we have.  Instead of having a transmitting tag, and multiple receiving beacons, it had multiple transmitting beacons and receiving tag which does all the math.  We decided that moving forward with this paper would not be productive, but it helped us decide to use a Kalman filter.   We then took a look at a different paper which had a similar hardware set up to our system and used a Kalman filter.

After looking at the other paper we decided that our approach should be to use Gauss-Newton to estimate the position and then use a Kalman filter to improve the accuracy.  So I then did research on Kalman filters, to understand generally how it works, and how we might apply it to our system.

Next week I will work on implementing the Kalman filter to improve accuracy of the location we predict.

Posted on

Team Status Report 3/29

This week we re-organized our rest of semester plan once again. Due to our advisers insisting we stick to executing our hardware plan.

Due to working from remote, we needed to find solderless headers which we had shipped from the UK. We are still awaiting our shipment of RPi4s.

Shiva was able to debug and fix the overflow issue he was having. He will take over figuring out the MCU–RPi interface portions from Rhea and run some tests to ensure consistency in measurements between anchor and tag.

Udit finished writing an ideal hardware timestamp simulator in Python.

Rhea and Udit spent the week reading 5+ papers on TDoA. The approaches that were considered were Iterative Hyperbolic Least Squares, Maximum Likelihood Estimator, Pseudo-Ranging, Weighted Delta-Range, Gauss-Newton Position Estimation, and Kalman Filter Smoothening.

We will be finalizing our research based on these approaches and picking a final approach to take by Monday.  We will implement these algorithms and test them using the hardware simulator (we will add in artificial hardware sampling and radio error) to get a clear idea of what accuracy we can achieve with different hardware errors. These will be used alongside the real measurements Shiva collects for Radio Delay to tell us how accurate our time-sync error must be.

Here is the updated Gantt Chart:

Gantt Chart V4 – Sheet1

Posted on

Udit’s Status Report for 3/28/20

This week I built our MVP for the hardware simulator. It visualizes one tag you can move with your arrow keys. It is paramaterized with ability to choose where anchors are placed and how often to send pulse the tags.

You can see a vague demo here:
https://1drv.ms/v/s!Aq6sdyvl6aqAn_EzuCtRUauMuckqig?e=53zhJC

As Rhea and I move into the main algorithm next week. Here is a TDoA overview of the general approach.

Rhea and I also read 3 papers for probabilistic approaches to TDoA that we are going to debate and refer as our primary approach tomorrow. Those papers methods are HLS and MLE, pseudo-ranging and weighted delta-range, and the most complex: kalman filter .

We are going to discuss and share our findings tomorrow. We will pick/combine approaches for our final implementation.

 

Posted on

Rhea’s Status Update 3/28/20

For the first half of this week I read papers on multilateration so we could pick a paper to reference when we start writing the algorithm for our system.  I narrowed it down to two possibilities, and we will choose which one to use as a group.

Towards the end of the week I received the solderless headers, so today I tried putting one of the headers on the chip.

The headers we got were a bit too big, so they needed snapped down to the correct size.

Once the header was snapped down to the correct size (it was one smaller than it should have been, but we’re not using the pins on the end) there was the issue of the chip not sitting flat on the acrylic, since it wasn’t long enough to have both bolts go through the holes.

So I decided to put the board on first, and then put the nut on, so the board would be a little more stable while I was hammering.  It still wasn’t entirely stable since there wasn’t anything on the left side, so trying to hammer in the left side was a bit difficult.

 

After trying to hammer it for about an hour in various different ways on various surfaces for increased stability, the top piece of acrylic slipped.  This somehow caused one of the rows of pins to be pushed further through the black thing, but not at all into the board.  Once this happened I decided to reconsider how to do this and try again tomorrow.

Next week I will get a header onto a board, and get the SPI communication working.  I will also work with Udit to plan how the multilateration software will be structured and start working on a portion of it.

Posted on

Shiva’s Status Update for 03/28

At the beginning of the week, I worked on implementing an ideal multilateration algorithm in Python, based on https://en.wikipedia.org/wiki/Multilateration#Cartesian_solution_with_limited_computational_resources.

Planning diagram I created for multilateration code

After Wednesday, based on Tamal’s concerns with our hardware implementation, I switched gears. I passed the multilateration software over to Udit for him to finish implementing and returned to the Decawave hardware to identify key metrics and details of how it tracks time.

From Wednesday through Saturday, I verified the conversion rate of Decawave time units to real-time seconds (1 DTU ~= 15.65 ps); identified the issue of timer rollover (the Decawave chip timer rolls over every 17.2 seconds), fixed the TDOA software so that the anchor now correctly reads the timestamp of pulse reception; implemented time conversion so that the software can display and log the timestamp in seconds, microseconds, and nanoseconds; and wrote a Python script to graph a single anchor’s measurements of when it receives pulses from a single tag.

Portion of output from timestamp logs for a tag and anchor at a fixed distance of 30 cm. Timestamps are displayed in hexadecimal DTUs, decimal seconds, and decimal nanoseconds.
Graph of pulse reception vs timestamp of reception for the full timestamp logs. Note the timestamp rollover, at pulse 60, from ~17 seconds back to 0 seconds.

Progress is still on schedule, though we’ve had to change some responsibilities around due to the COVID-19 crisis. In particular, Rhea and Udit are now working on the multilateration software. For next week, I will verify the accuracy of the Decawave chip timestamps, then collect sample timestamp measurements using the Decawave chips at various distances to plug into Udit’s simulator.

This was a bit of a hectic week and our Gantt chart will need some re-adjustments. In particular, I’m working with anchors now instead of Rhea.
Posted on

Udit’s Status Report for 3/21/20

Pre-spring break I had been doing a lot of work into helping program the TDoA anchor code with shiva but that work became put on the backburner with the changes to our project due to COVID

I spent this week, thinking about the software for my simulation. I will work on converting it into a block diagram soon. But here is the jist of it.

  • Build a grid-based approximation of a basketball court. Hardcode placement of anchor objects on the edges of the court. Have tags in the grid on the court moving around semi-randomly as well as user controlled.
  • Use the distances between tags and anchors to calculate a time to travel between them. Use that plus a single centralized time-stamp (i.e. assuming perfect time sync) to generate a perfectly accurate time stamp for each anchor per tag pulse.
  • Use sockets to forward these timestamps to the localization software.
  • Log actual locations for comparison with the calculated locations by multilat software.

There a bunch of reach features that would be useful to have after the MVP described above. This includes a GUI for the bball court virtualization and adding in simulated hardware error. There would be a separate errors for radio transmission delay, anchor time-sync error, and LoS blockage delays.