Posted on

Andrew’s Status Report for Feb 24

Personal tasks of this week:

Task: Preliminary Circuit Simulation:

Definition:  According the Sergey’s thesis, the theoretical circuit primitives were found to model the mathematical constraint. However, the circuits need to be modified to realize the theoretical circuit, as it contains ideal circuits that don’t exist in the real world.

Completion: The task is partially completed.  The circuit was researched and equivalent components from the thesis that can be sourced now were found for each component.  The circuit was attempted first in PSpice, but decided to transition into using LTSpice, as we realized the speed of learning and prototyping ability of LTSpice was much more important given our time constraints compared to the features available on PSpice. A basic schematic was built for each primitive, but has not been tested extensively for the simple optimization circuit

Next Steps:

The next steps are to use PSpice to create the simulation of the simple optimization circuit and verify if the minimum energy state converges to the expected solution.

Overall progress assessment:

My progress is slightly behind-schedule, as I still need to finish up the optimization circuit, but it should not be that difficult to catch up, as the components have already been selected and imported.

 

Posted on

Team Status Report for Feb 24

Significant risks and risk management:

Risk: The analog circuit can’t meet the required tolerances

Definition: This risk has been brought to our attention by our assigned in instructor Thomas Sullivan (Thanks!). It is currently unclear to us what tolerance the analog components will need to have in order to satisfy the 10% solution accuracy required by the accuracy requirement (NR3). This is nontrivial to determine as the accuracy of the whole circuit can’t be easily associated with the accuracy of individual components.

Severity: If the analog circuit can’t meet the required tolerances, the progress of the whole project would be severely jeopardized, because the accuracy requirement (NR3) would not be satisfied.

Resolution: A solution is to use Sergey’s work [1] as a reference. If our components are more accurate than Sergey’s components in every relevant measure, it is likely that the whole circuit wouldn’t be significantly worse in accuracy compared to his circuit. This is possible because  more accurate components are available since his work was published.

Current progress:

We have completed P2, and is currently working towards P1 and P3. We performed some benchmarking on P2, with results showing that the majority of the time spent in the solver is on the QP subproblem(32ms out of 38ms). This means that if we solve the QP subproblem with our analog solver we can potentially get large speed up.

Changes to the existing design:

There are no changes to the existing design. We have completed P2 successfully, indicating that we can proceed with our existing design.

Changes to the project schedule:

Similarly, there are no significant changes to the project schedule.

Posted on

Alvin Zou’s Status Report For 2/24

Personal tasks of this week:

Task: Profiling double pendulum swing up with NMPC

Definition: Analyzing results from the double pendulum swing up and performing performance profiling.

Completion: I have conducted some profiling on the performance of the NMPC controller, with results showing that most of the time spent in the pipeline is on solving the QP subproblem. This confirms the hypothesis that we can theoretically achieve a lot of speed up if the QP subproblem is solved using our analog solver.

 

Task: Design review presentation

Definition: Presenting the design review presentation

Completion: The presentation is completed.

 

Task: Formulating NMPC problem and isolating the QP subproblem

Definition: Formulating the NMPC problem for our system mathematically and converting it to a form that can be solved by SQP. After this is achieved, the QP subproblem can then be isolated. This step is to calculate what variables are used in the QP subproblem, so that the analog circuit can be designed to solve the correct subproblem.

Completion: The state update equations have been formulated. Next is converting the equations into a form that can be solved by SQP and then isolating the QP subproblem.

 

Next Steps:

The next step is to continue deriving the mathematical representation of the NMPC problem to eventually isolate the QP subroutine in preparation for replacing it with our analog solver.

Overall progress assessment:

Currently on schedule. Working towards isolation of the digital and analog solver.

Posted on

Thomas’s Status Report for Feb 24

Personal tasks of this week:

Task: Library-Based NMPC Swing-Up Controller Benchmarking

Definition: Run a performance benchmark on the library-based NMPC swing-up controller, measuring the time it takes to complete each step of solving the NMPC problem, and identify the performance bottleneck of the system.

Completion: The task is completed. We benchmarked the swing-up controller and found that 32ms out of 38ms in each iteration is spent on solving the NLP, which can be accelerated using our proposed analog SQP solver to achieve significant speedup.

Task: Symbolic NLP Formulation of the NMPC Swing-Up Controller

Definition: Symbolically formulate the NMPC Swing-Up controller as an NLP, which acts as the NLP problem we supply to the analog SQP solver on each iteration.

Completion: The task is partially completed. We’ve made substantial progress in deriving the dynamics constraints and symbolic cost function. More work will be done in the next week.

Next Steps:

My next step is to continue working on formulating a symbolic NLP problem of the NMPC swing-up controller. I will also continue to work with Andrew on analog component selection and circuit simulation.

Overall progress assessment:

My progress is on-schedule, as all of my tasks this week have been completed or partially completed.

Posted on

Team Status Report for Feb 17

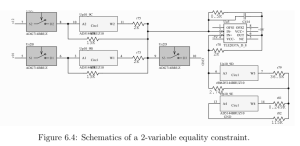
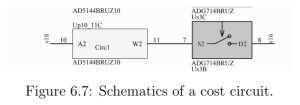
Significant risks and risk management:
Risk: Inverted double pendulum simulation has insufficient numerical accuracy for NMPC
Definition: Since running the NMPC controller might require a higher numerical accuracy than simulating the dynamics of the inverted double pendulum system, the numerical accuracy of the system might be insufficient when NMPC is integrated into the symbolic simulation.
Severity: If the numerical accuracy is insufficient, the progress of the whole project would be severely jeopardized, because the system would likely not satisfy NR3 (accuracy).
Resolution: We will try to mitigate the risk by synthesizing a NMPC controller that has sufficient robustness against noise, because numerical inaccuracies can usually be seen as noise from the controller’s perspective.
Changes to the existing design:
There are no significant changes to the existing design as we’ve just started implementation.
Changes to the project schedule:
Similarly, there are no significant changes to the project schedule

Additional Societal Impacts

Part A)

Optimization is a powerful tool of representing real-world problems mathematically, and fast solvers, like the product we aim to deliver, make solving them easier.

Health

Optimization helps make healthcare more efficient and accessible. For example, finding the most efficient distribution of vaccines during a pandemic can be formulated as an optimization problem. Solving this problem quickly can enable more effective control of infectious diseases.

Safety

Optimization helps make vehicles safer to operate. Vehicle control with safety guarantees is a classic application of model predictive control (MPC), which is an optimization problem. Our solver has the potential of solving MPC problems in real-time, which can make vehicle control strategies with stronger safety guarantees practical.

Welfare

Optimization helps distribute scarce resources efficiently. Logistics is another classic application of optimization, which is critical for fulfilling everyday needs, especially during periods of hardship. Solving these problems efficiently ensures that goods and services are delivered where they are most needed.

Part B)

Our analog SQP solver has potentially wide societal implications. This comes from the fact that SQP solvers are used to solve nonlinear optimization problems, which is general class of problems with extensive use cases and applications, spanning from computer science to machine learning to biology and medicine(examples can be found in https://neos-guide.org/case-studies/). Because of the breadth of possible applications, our product solution can potentially affect a large group of people.

In particular for social groups, solving optimization problems can help make management in large organizations more efficient. One example is in the supply chain industry, where creating a supply chain strategy that operates across multiple regions can be formulated into an optimization problem.

Part C)

Our applications in analog optimization have significant implications in terms of the related economic factors. Specifically, this is because each of the systems relating to the production, distribution, and consumption of goods and services are areas that can be optimized to be more efficient, which leads to savings in terms of time and money. Furthermore, optimization enhances the general productivity of our society by making production procedures faster, cleaner, safer, and more efficient. As a result, a productive society leads to more sustainable development and more safer environment.

*In the team report, A was written by Thomas Liao, B was written by Alvin Zou and C was written by Andrew Chong.

Posted on

Andrew’s Status Report for Feb 17

Personal tasks of this week:

Task: Trade Studies on PCB Manufacturing/Assembly

Definition: There were many considerations in choosing a PCB Manufacturing/Assembly company to manufacture our product. This includes quality, turnaround time, ability to assemble the PCB components, and cost. We considered the following companies: JLCPCB, PCBWay, OshPark, and Colorado PCB Assembly.

Completion: The task is completed.  From our trade study, we were able to determine that PCBWay was the best manufacturer for us. This is because PCBWay generally has good quality, has the ability to both PCB manufacturing and Assembly together, has turnaround + shipping in approximately a week, and offers large discounts if the Assembly service is used. In fact, we found that if the Assembly service is used, the price is actually cheaper than buying a stencil and manually reflowing it ourselves, which can introduce a source of error. Some reasons why we didn’t pick the other companies are as follows: JLCPCB has poor quality, OshPark can only manufacture the PCBs, and Colorado PCB Assembly, while with very high quality and fast turnaround, only offers assembly. While it is possible to combine multiple options, we thought that with the component sourcing to different parts, as well as PCB shipping from the PCB manufacturer to the Assembly, back to us would be worse both logistically and for our schedule.

Task: Preliminary Design for Optimization Prototype

Definition: To ensure that we are able to complete the final prototype of the analog optimization circuit, a smaller, proof-of-concept prototype must be made in order to ensure that our approach is sound.

Completion: The task is completed.  Looking through Sergey’s Thesis, we found that there is a schematic provided for a simple 2-variable equality constraint, a 2-variable inequality constraint, and a cost function constraint (which is just a series of resistors) that we can use as our basis for our preliminary prototype. However, the problem is only for a 2-variable equality constraint. We decided to make a slightly more complex design and make the simplest possible optimization circuit with one equality constraint, one inequality constraint, and one cost function.

Next Steps:

The next steps are to use the tools selected to create a prototype of our simple optimization problem, as detailed in Sergey’s thesis as a proof of concept, then Once the baseline works, we will begin expanding that into creating our first prototype analog circuit that specifically models our double pendulum swingup optimization problem. Once that is done, we will order using PCBway.

Overall progress assessment:

My progress is on-schedule, as all of my tasks this week have been completed.

 

Posted on

Alvin Zou’s Status Report For 2/17

Personal tasks of this week:

Task: Double pendulum swing up with NMPC

Definition: Building Prototype 2 by creating a double pendulum system, designing a controller to control the system, and visualizing the simulation.

Completion: Currently, I have created the system and designed a controller with Thomas using do-mpc that can successfully swing up the pendulum.

Task: Slides for design review presentation

Definition: Creating the slides for the design review next week with the rest of the team. Also rehearsing for the presentation.

Completion: The presentation is mostly completed. Aim to complete by Sunday.

 

Next Steps:

The completion of P2 has validated the problem can be solved using a software SQP solver. The next step is then to isolate the QP subroutine in preparation for replacing it with our analog solver. Basic profiling should also done on P2 to collect performance data.

Overall progress assessment:

Currently on schedule. P2 is completed.

Posted on

Thomas’s Status Report for Feb 17

Personal tasks of this week:

Task: Library-Based NMPC Swing-Up Controller Synthesis

Definition: Using an open source library, synthesize a NMPC controller that is capable of swinging up an inverted double pendulum. The purpose of this task is to validate that swinging up the inverted double pendulum is achievable with NMPC with small prediction and control horizons. The implementation must be in Python in order to integrate with the rest of the project.

Completion: The task is completed. We’ve selected do-mpc [1] as our library due to its ease of use. The synthesized NMPC controller is capable of consistently swinging up an inverted double pendulum with a prediction horizon of 3 and a control horizon of 3. However, we will synthesize a controller with longer predilection and control horizons for better robustness against noise.

Next Steps:

My next step is to integrate the NMPC swing-up controller with the symbolic dynamics model, and derive a symbolic NLP problem that corresponds to the NMPC controller. Then I will work on solving the NLP problem by implementing the SQP algorithm, calling an open-source QP solver.

I will also work with Andrew on analog component selection and circuit simulation.

Overall progress assessment:

My progress is on-schedule, as all of my tasks this week have been completed.

References:

[1] https://www.do-mpc.com/en/latest/

Posted on

Andrew’s Status Report for Feb 10

Personal tasks of this week:

Task: Literature Review

Definition: By studying Sergey’s Thesis more closely, our aim was to look for methods in which we can further flesh out or improve our design.

Completion: The task is completed. By taking a closer look at the thesis, we were able to discover the primary accuracy and performance concerns of the system. These are the nonlinearity of the potentiometers contributing to a decrease in accuracy, as well as the negligence of parasitic capacitance contributing to a decrease in performance. More specifically, in Sergey’s PCB design, due to an oversight in the parasitic capacitance, it caused his system to develop non-stable behavior, which required him to add compensating capacitors to the feedback loop of his op-amps. If these were considered,  the step response could have been significantly improved as shown below.  By learning from mistakes in the original designs like these, we believe that we will be able to achieve solid performance. Furthermore, this research was very helpful in determining which component aspect we should put the most focus on.

Source: https://www.sciencedirect.com/science/article/abs/pii/S0098135414000131

Task: Spice Selection

Definition:  To begin circuit simulation, a spice tool would be required to test the behavior of our preliminary circuits. Considering the wide variety of spice tools available, a detailed review of each of the available products was done.

Completion: The task was completed. We have decided on using Cadence’s PSpice considering its performance, as well as the fact that it is readily available to CMU students. The contender was AltiumSpice, as our PCB design will be in Altium, so it would be easy to integrate. However, we decided against it considering its performance.

Task: Preliminary Part Selection

Definition: Considering our current requirements, a preliminary selection of our main components was needed to determine if we would be able to deliver the desired performance with the required performance and accuracy.

Completion: The task is partially completed. By using the same components that Sergey used as a baseline, we looked for components that had tolerances and performance that was at least as good, or better. Considering the developments in the industry, we were able to make a shortlist of parts that we are considering, but have not determined the specific components we are using yet.

Overall progress assessment:

My progress is on-schedule, as all of my tasks this week have been completed. I will continue working towards completing my Prototype of creating a  circuit simulation of a simple optimization problem.

 

Posted on

Team Status Report for Feb 10

Significant risks and risk management:

Risk: Inverted double pendulum simulation wouldn’t converge

Definition: Since we are still working on building a simulation for the inverted double pendulum, we do not know whether or not problems like numerical instability or truncation error of the integrator would cause the simulation to not converge, i.e. incapable of settling on a solution.

Severity: If the inverted double pendulum simulation wouldn’t converge, the progress of the whole project would be severely jeopardized, because the simulation is a critical part of Prototype 1, that is swinging up the double pendulum with NMPC in simulation.

Resolution: A step we can take right now is to accelerate our progress towards a testable MVP of the simulation, whose convergence can be validated. Another measure is to study the properties of common numerical integrators and select those with superior convergence properties and are available in our library.

Risk: The analog circuit can’t meet the required tolerances

Definition: This risk has been brought to our attention by our assigned in instructor Thomas Sullivan (Thanks!). It is currently unclear to us what tolerance the analog components will need to have in order to satisfy the 10% solution accuracy required by the accuracy requirement (NR3). This is nontrivial to determine as the accuracy of the whole circuit can’t be easily associated with the accuracy of individual components.

Severity: If the analog circuit can’t meet the required tolerances, the progress of the whole project would be severely jeopardized, because the accuracy requirement (NR3) would not be satisfied.

Resolution: A solution is to use Sergey’s work [1] as a reference. If our components are more accurate than Sergey’s components in every relevant measure, it is likely that the whole circuit wouldn’t be significantly worse in accuracy compared to his circuit. This is possible because  more accurate components are available since his work was published.

Changes to the existing design:

There are no significant changes to the existing design because this is the week in which our proposal was presented, and our initial design was just finalized.

Changes to the project schedule:

Similarly, there are no significant changes to the project schedule compared to what was presented in the proposal presentation.

References:

[1] https://escholarship.org/content/qt01q7h2ng/qt01q7h2ng_noSplash_2892dd43015926698bb02bdb85d7b62f.pdf