This week I made an update on Chess Game logic to make testing easier. I added some modules that make changes on the board state, return selected positions, and checks the empty spaces, to help the testing process. I also include test cases on the test bench.
I also focused more on CV this week. I concentrated on detecting the coordinate of the board where a change has been made, while Anoushka focused on the better quality of grid lines through neural net training. The quality of initial sample images were not good enough for detecting changes, since the coordinate of the board center was inconsistent throughout the states. The previous sample photos had inconsistent grid lines, which made change detection impossible. So I took another sample photos at a lab on Wednesday in a more consistent setting with camera held in one place. I edited new sample photos through CV so that the coordinates of each square is aligned.
I also made an update on Hough line threshold Anoushka’s code that get the gridlines from edge detection so that the correct grid lines will be generated from more varying photos. The most significant obstacle from our CV change detection is inconsistent reflection on our board. Since our physical board is made out of glassy acrylic material, anything that gets in the way between the light source and the board gets reflected on the board (such as user’s hand, camera, user’s hair and etc).
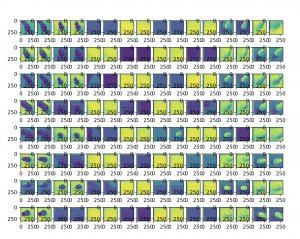
From the photo above, change detection module should output coordinate (4, 4) and (4, 6). However, no matter what method I try, (abs diff, structural similarity, background subtraction method on grey scale, RGB scale, HSV scale) threshold could not separate coordinates without changes from coordinates with changes, because the output difference value of the coordinate with different reflection on the acrylic piece was too high.
This is a huge problem in our CV because reflection on our board is going to be inconsistent throughout the whole game. I updated a working code that computes the difference with limited size of the square (at center) so that it can disregard difference from background reflection. However, this code will not work if the user places a piece away from the center of the square. The other solution will be to remake the board with an unreflecting material, such as silicon. For another solution approach, both me and Anoushka tried to blur out the reflection, but was not achievable.
Next week I will mainly focus on coming up with a solution approach to this reflection problem and to come up with a stable change detection algorithm.
