Overall question hint: Wolfram
Alpha can be a useful resource. Be EXTREMELY careful of numerical round-off
errors for very low probilities that will cause incorrect answers. Forget about
Excel (don't believe us? try it and see if it matches Alpha results). Some
calculators can have problems as well. Always use Wolfram Alpha or another
high-precision calculation tool to check your answers. Remember that we just
learned about the pitfalls of floating point math. Don't let them bite you
here!
27-1: Consider the below reliability calculation example:
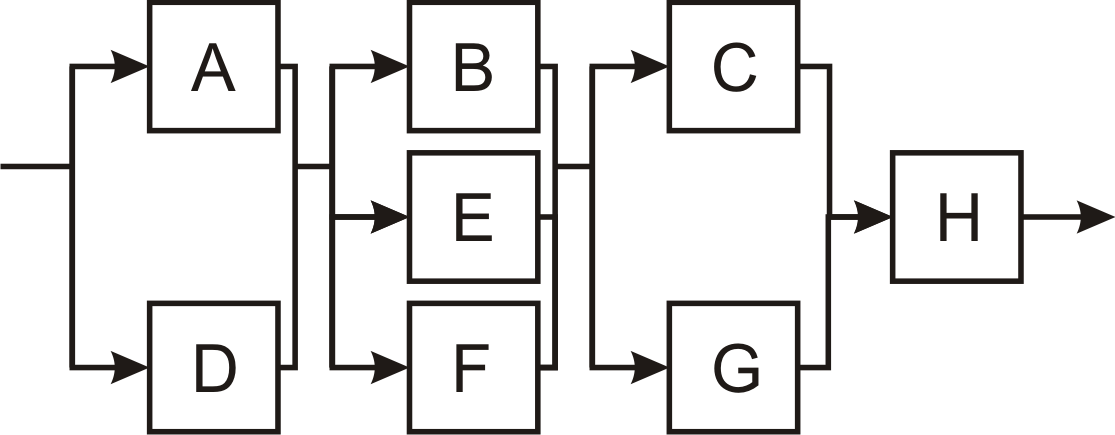
- Assume a t=100 hour mission and the following values for mean time to
failure:
- A=1000 hrs
- B=1500 hrs
- C=2000 hrs
- D=900 hrs
- E=100 hrs
- F=90 hrs
- G=2500 hrs
- H=9000 hrs
Hints:
- Break the calculation up into steps
- Generally you'll alternate a step that is computing R(t) of a component, or
a step that computes R(t) for chunks of the system already analyzed
- Work from the "inside out," for example starting with nodes B, E
and F, and then using that as a logical component as part of the series chain.
- Use Wolfram Alpha if there are a lot of 9s involved. (Hint: there will be a
lot of 9s involved.)
- Keep track of each step on your hand-line slide as a way of showing your
work. Paste numbers in from Wolfram Alpha. (Don't use a spreadsheet -- you'll
get too much round off error). Here are some steps to get you started:
- R(B)=_____
- R(E)=______
- R(F)=______
- R(B || E || F)=______
- ...
- R(A||D) --- R(B||E||F) --- R(C||G) --- R(H)=_____________
27-2. Consider a two-engine passenger aircraft. Modern commercial passenger
aircraft are designed to be able to fly and land even if only one engine is
working. Assume that each engine has an in-flight failure rate of one failure
per 51,000 hours (this is an actual number for a particular engine used on a
commercial 2-engine aircraft). The FAA requires an aircraft to have a
probability of catastrophic failure (e.g., both engines shut down) of less than
1e-9 (one catastrophic failure per billion hours). Assume random independent
failures. While in operation pilots will attempt to restart an engine, the
calculations conservatively assume that once an engine has shut down it cannot
be restarted due to an internal fault.
- 27-2a. What is the reliability of the aircraft in terms of
probability of both engines failing during a 12 hour trans-Pacific flight? Put
your final answer in terms of 1 failure out of X flights. (Show your work)
- 27-2b. What is the chance that the aircraft loses only a SINGLE
engine during a 12-hour flight? (1 failure out of X flights)
- 27-2c. Assume that after a single engine failure the aircraft
diverts to the nearest airport that is 3 hours away. What is the probability
that this one engine will still be working when the aircraft lands 3 hours
later? (1 failure out of X such 3-hour flights)
- 27-2d. Briefly explain the concept of ETOPS-180 operation for
aircraft. (For this particular question Wikipedia is an acceptable
source.) Pasting in a picture that illustrates the concept.
- 27-2e. Given the previous answers, what is the probability of
catastrophic aircraft loss (crashing because of loss of both engines) if
ETOPS-180 rules are followed? (1 failure out of X flights)
- 27-2f. Is this engine reliable enough to meet the 1 catastrophic
failures per billion flight hours with ETOPS-180 flight rules assuming that all
missions are 12 hour flights?
Rubric:
- Slide #1: line-by-line calculations for 27-1, ending with total
reliability. A photo of LEGIBLE hand-written work on paper or a whiteboard
pasted into a slide is acceptable.
- Slide #2: Answers to 27-2a through 27-2c. (OK if they spill onto an extra
slide.) Show your work (photo pasted in is acceptable)
- Slide #3: Answers to 27-d through 27-2f. (OK if they spill onto an extra
slide.) Show your work (photo pasted in is acceptable)
Supplemental Material:
