Carnegie Mellon University

Department of Electrical and Computer Engineering

18-200 Fall 2000

Mathematical Foundations of Electrical Engineering

Problem Set 9 (last one!)

Issued: Tuesday, December 5

Due: Tuesday, December 12 by 4:30 PM (absolute deadline) in HH B205

NOTE: The final exam will be given on Thursday, December 14 from 5:30 - 8:30 PM in PH100.

Problem 1: Two vectors, A and B are given by:

A = 3a_x + 6a_y – 2a_z

B = – 2a_x + 5a_y – 3a_z

a) Find the dot product A · B

b) Find the angle a between A and B

c) Find the cross product A x B

d) Show that the magnitude of the cross product you found in part c) satisfies:

|A x B| = |A| |B| sin(a)

Problem 2: A scalar field, U(x, y, z) is given in rectangular coordinates by:

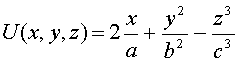
Where a, b, and c, are known constant distances.

a) Find the vector field that is given by:

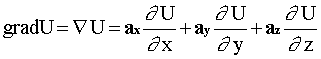
b) Calculate the line integral:

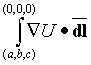
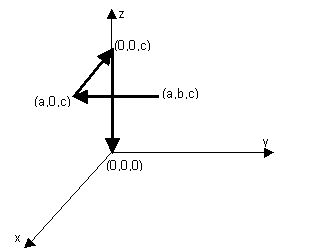
For the path shown in the figure below. The path starts at point (a,b,c) and follows a straight line back to point (a,0,c), then follows a straight line back to point (0,0,c), then follows a straight line down to point (0,0,0).

c) Show that your result from part b) is identical to the difference between the value of the field U at the end point of the line integral and the value of U at the beginning point of the line integral, i.e., show that:

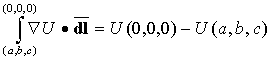
Problem 3: A vector function of space, F(x,y,z) is given by:

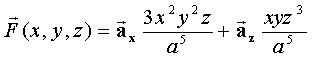
Where “a” is a known constant distance.

a) Find the scalar function of space that is defined by:

b) Calculate the volume integral:

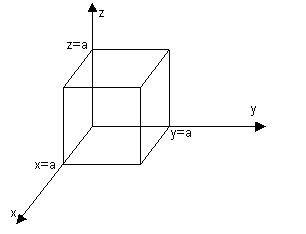
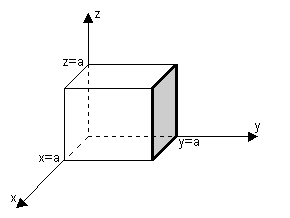
For the volume shown in the figure below. The volume is a cube with faces at x=0, x=a, y=0, y=a, z=0, and z=a.

c)Evaluate:

i.e., the component of F in the direction of the outward normal (the subscript “n” denotes “normal”) on each of the six faces of the cube (top, bottom, left, right, front, and back). Show that your result from part b) is identical to the total outward flux of F through the surface of the cube, i.e., show that:

Problem 4: For the same vector function F of space that is given in problem 3:

a) Find the vector function of space that is defined by:

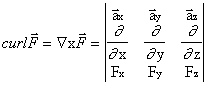
b) Consider the open surface shown in the figure on the next page. The surface is a square in the plane y=a, with edges x=0, x=a, z=0, and z=a. Evaluate:

i.e. the component of the curl F in the direction of the normal pointing out of the square surface in the positive “y” direction. Then, over the square, calculate this surface integral:

c)

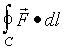
Calculate the line integral:

in the counter-clockwise direction for the closed contour that consists of the edges bound by the open square surface as viewed from the front. Show that your result from part b) is identical to the total circulation of F around the closed contour that bounds the open surface, i.e., show that: