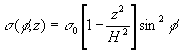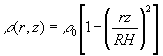Carnegie Mellon University

Department of Electrical and Computer Engineering

18-200                                                                                                               Fall 2000

Mathematical Foundations of Electrical Engineering

Problem Set 8

Issued: Thursday, November 16

Due: Thursday, November 30

 

Note:  For this problem set, you may want to refer to an integral table (these are generally found in an appendix of a calculus book, etc.).  On an exam, if we feel you may need an integral table, we’ll include one for you with the exam.

 

 

 

 

1.        Solve the following sets of differential equations with initial conditions:

 

a) 

 

 

  dy1(t)/dt  =  3 y1(t)  +   2 y2(t)   ;     y1(0)  =  6

 

  dy2(t)/dt  =  - 4 y1(t)  -   y2(t);            y2(0) =  0

 

 

 

b)

 

  dy1(t)/dt  =  15 y1(t) -  15 y3(t)     ;                     y1(0)  =  0

 

  dy2(t)/dt  =  -3 y1(t)  +  6 y2(t)  +  93(t);             y2(0) =  -3

 

  dy3(t)/dt  =  5 y1(t)  -  5 y3(t)     ;                        y3(0)  =  4

 

 

 

 

c)

 

  dy1(t)/dt  =  8 y1(t)  +  3 y3(t)     ;       y1(0)  =  15

 

  dy2(t)/dt  =  2 y1(t)  +  2 y2(t)  +  y3(t)    ;          y2(0) =  9

 

  dy3(t)/dt  =  2 y1(t)  +  3 y3(t)     ;                       y3(0)  =  -2

 

 

 

 

2.        A volume charge density r(x, y, z) is distributed over the volume of a rectangular solid that extends between x = 0 and x = a, between y = 0 and y = b, and between z = 0 and z = c.  The functional dependence of r(x, y, z) upon position within the volume is:

 

 

where ro is a known constant with units C/m3. 

 

Find the total charge Q within the rectangular solid.

 

 

 

3.        A certain antenna emits a power per unit area that varies with position in the region that surrounds the antenna. In a spherical coordinates system whose origin coincides with the center of the antenna, the power density propagates radially outward, and takes the form:

 

 

where P0 is a constant with units Watts and r and q are spherical coordinates.

 

By integrating the power per unit area over the surface of a sphere that surrounds the antenna, find the total power P that radiates outward from the antenna.

 

 

 

4.        A surface charge density s(f, z) is distributed over the side-wall of a circular cylinder whose axis is the z-axis, has radius R, and extends between z = 0 and z = H.  The functional dependence of s(f, z) upon angular position and height on the surface is:

 

 

where so is a known constant with units C/m2. 

 

Find the total charge Q on the side wall of the cylinder.

 

 

 

5.        A surface charge density s(f, z) is distributed over the surface of a cone with height H and base radius R  The cone is oriented "upside down" in a cylindrical coordinate system so that its tip is at the origin and its base is at z=H. The functional dependence of s(f, z) over the surface of the cone is:

 

 

where so is a known constant with units C/m2. 

 

Find the total charge Q on the surface of the cone.

 

 

 

6.        A volume charge density r(r, q) is distributed within the volume of a spherical shell with the inner radius a and the outer radius b (no charge exists in the inner sphere). The functional dependence of r( r, q) upon radius and angular position with respect to the vertical axis is:

 

 

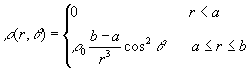
where ro is a known constant with units C/m. 

 

Find the total charge Q within the sphere.

 

 

 

 

7.        A volume charge density r(r, z) is distributed within the volume of a cone with a flat base of radius R that sits at z = 0 (i.e., in the horizontal plane which cuts through the origin of the z-axis) and tapers off to a radius of zero at z = H.  The functional dependence of r(r, z) upon position within the volume  is:

 

 

where ro is a known constant with units C/m3. 

 

Find the total charge Q within the cone.